How can we create a generation of brilliantly innovative kids?
And let's be clear: this is the purpose of our school. We're going to spend a lot of time learning about the past, and recapitulating its greatest accomplishments, but this is all toward the goal of doing new things in the future.
As the Renaissance reader, writer, and thinker Salutati wrote:
I have always believed that I must imitate antiquity
not simply to reproduce it,
but in order to produce something new.
So how do we create this generation of brilliantly innovative kids?
First, we have to understand the nature of creativity.
Then, we need to build it into every piece of our school.
It's a professional nuisance, I suppose, that I end up hearing so much nonsense about creativity. Most educational innovators drivel on about "creativity", rarely defining the word (often it seems to mean anything to do with art) and trusting that creativity is natural.
The assumption seems to be that if you just "let out" the native forces of a child, creativity will result.
Well, sometimes. But not frequently.
At least, new, good ideas don't just spill out all by themselves. (Unless the kid is some kind of creative genius, in which case, why do we have them in a school at all?)
That's not to say that you force creativity. Typically, you don't — forcing doesn't get you innovation. Rather, new, good ideas take cultivation — they pop up in certain contexts, and not others. Get the environment right, and you'll get innovation.
What environment is that?
Steven Johnson wrote the book on this: Where Good Ideas Come From: A Natural History of Innovation. His major idea:
Don't think of creativity as forging new ideas by yourself.
Think of creativity, rather, as piecing together others' ideas to make something new.
Johnson:
We have a natural tendency to romanticize breakthrough innovations, imagining momentous ideas transcending their surroundings, a gifted mind somehow seeing over the detritus of old ideas and ossified tradition.
But ideas are works of bricolage; they're built out of that detritus. We take the ideas we've inherited or that we've stumbled across, and we jigger them together into some new shape. (pp. 28–28, emphasis mine)
(Ooh — there's an RSA Animates for the book! Enjoy the next four minutes and six seconds of your life.) Johnson continues:
The trick to having good ideas is not to sit around in glorious isolation and try to think big thoughts. The trick is to get more parts on the table…. A good idea is a network. (p. 42 & 45)
Creative students are network-builders. They take scads of other data, and combine them together in new ways. A limiting factor, then, is how many ideas they can stumble across! We need our school to be as idea-thick as possible.
I hope it's apparent that we're planning to do just that — crowd our school with stories and thoughts and questions and images and facts and plenty of other abstract nouns I'm forgetting.
And those from as many disciplines as possible — chemistry and religion and art and math and music and biology and everything. Narrow disciplinary boundaries are the death of innovation (at least in K-12 classrooms).
Immerse our kids with wonderful and diverse content — one of the keys to prompting creativity.
But — if only ensuring creativity were so simple! Because here we run smack into a big problem; in fact, a fundamental cognitive limit.
Creativity is connecting, and the easiest place to connect ideas is inside your own head. We pull information — ideas, stories, facts, questions, images, whatever — out of our long-term memory, and connect it with whatever new thing we're looking at.
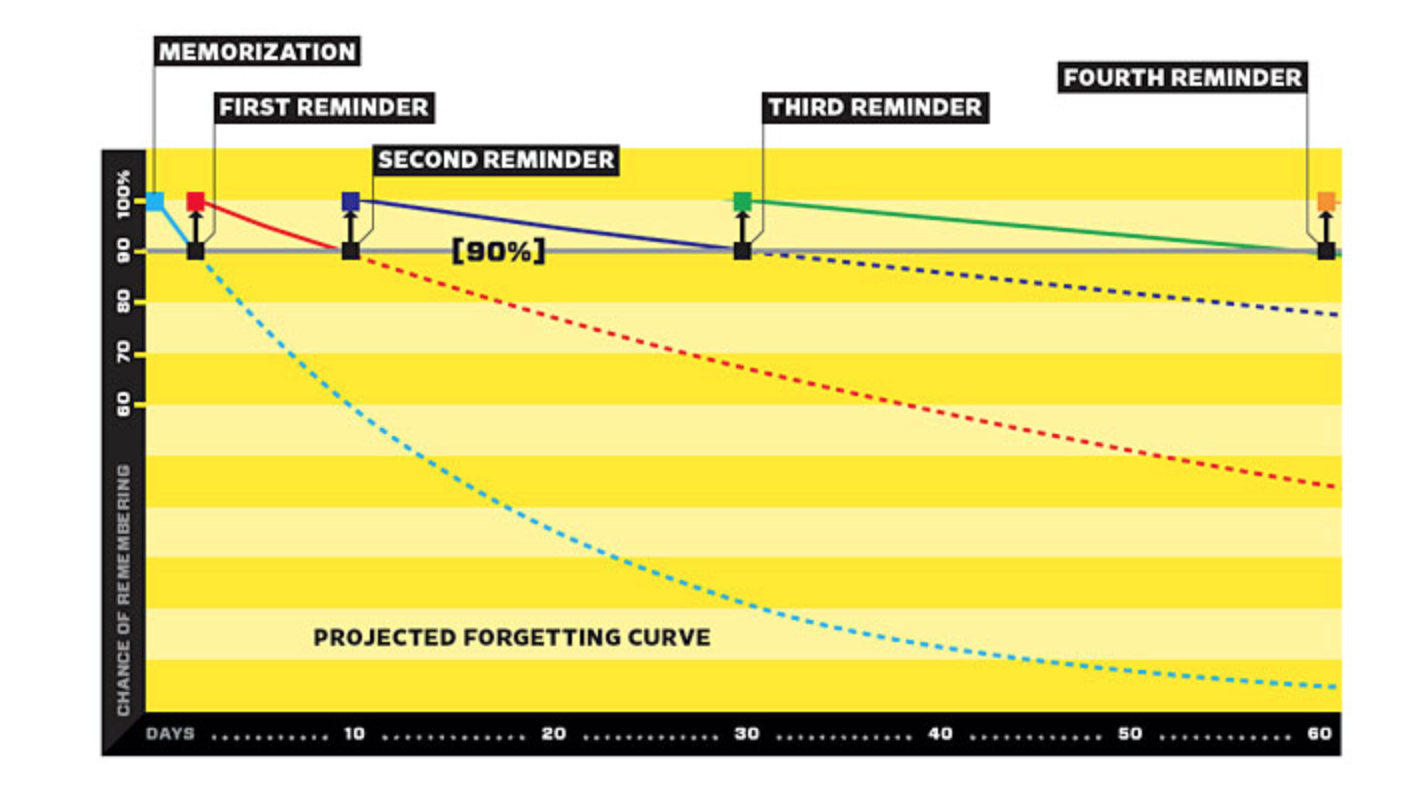
The trouble is that it's easy — scandalously easy! — to misplace the memories in your long-term memory.
We all know this, of course. You've learned far, far more about (say) the Civil War than you're aware of right now. Much of that knowledge is still inside your skull, somewhere. If you heard it again, you'd recall that, yes, you'd heard it before. But you couldn't have said what it was. The knowledge was more or less useless to you.
This is the Tragedy of Long-Term Memory. (Well, it's one of the tragedies. The other is that you just plum forget things. More on that, and how to overcome it, in a later post.)
And some people fall prey to this tragedy more than others. Some people are simply worse at making these connections — they can't access their long-term memories as quickly, can't hold as much data in their working memories (more on this later) to juggle the ideas around.
So we're in danger of privileging some of our students over others. To some extent, this is unavoidable — but we should look for tools that will equalize the playing field.
Delightfully, there's a fix! And this fix revolutionized human society: write ideas down.
Paper is the original creativity-extender. (Well, clay tablets, but nuts to the Sumerians!) Writing things down offloads the memory. We can think just by leafing through a notebook. Of course, there is the occasional glitch:
Professor Henry Jones: Well, he who finds the Grail must face the final challenge.
Indiana Jones: What final challenge?
Professor Henry Jones: Three devices of such lethal cunning.
Indiana Jones: Booby traps?
Professor Henry Jones: Oh, yes. But I found the clues that will safely take us through them in the Chronicles of St. Anselm.
Indiana Jones: [pleased] Well, what are they?
Indiana Jones: [annoyed] Can't you remember?
Professor Henry Jones: I wrote them down in my diary so that I wouldn't have to remember.
But that trouble seems more limited to international adventurers than to K-12 students.
Except maybe it's not.
I want to point out that I'm not just blasting conventional schools, here. I'm rather tickled that schools make use of one of humanity's most time-tested cognitive tools! But why don't school notebooks, as they're popularly used, increase creativity?
Three reasons, I think.
First, creativity isn't part of the curriculum. Many classes don't ask students to think new thoughts — and when they do (English essays, for example), they don't train students in how to cobble together old ideas to make new ones.
Second, the notebooks aren't used for creativity. Notebooks are seen as places to dump data, and maybe review it before a test — not places to access again and again to get new insight.
Third, when was the last time you looked through your school notebooks? You can cheat for this one, and include your college notebook. Did you leaf through them in the last month? Less than a year ago? I didn't think so. (And neither did I — and I kept mine!) We dump data in, and then let it moulder there.
There's a solution to this. Well, actually there are a number of solutions to this — but I want to outline just one today:
Externalize knowledge.
Splay it on the walls.
One major purpose of classroom walls is to store information. Interesting information. Beautiful information. Information that students value, and which can help them think new thoughts in the future.
The walls can take on some of the role of long-term memory.
Information on the walls can be casually referenced in class. Students can browse the walls when they're stuck for an idea.
Of course, we can't fit all of the information students learn on the walls — only the most meager sliver of it. But that's all we need: we can fill the walls with triggers for what the class has already learned.
Triggers for what they've already learned: that seems a crucial piece. It's not that we'll put new information on the walls. That'd be stupid. New knowledge is best learned through other people (and experience, and books, and any number of other things). It's not best learned through truncated bits of information hung on a wall.
But the walls can display bits of information that students have already learned — bits that trigger complex recollections.
At the beginning of the year, much of the wall-space of a classroom, therefore, will be empty. As the classes move on, we'll gradually fill the walls until the room becomes an index of what's their heads.
I say "index" — but it can be thought of as a sort of machine, with students the moving parts. They'll walk around, connecting an idea here (next to the wind0w) with a question there (above the sink), comparing it all to a story there (behind the plants).
Students must play a hand in construction of this — they can deliberate as to what to put on the wall. It's an externalization of their knowledge, after all.
But I have to apologize: this probably seems entirely abstract. Next, I'll hope to give an example of one type of information we can put up — a "wall of talking dead people" — and what we can do with it — practice moral creativity.