Can you solve this?
Sketching out our liberal-arts-major thoughts on what math in a new-kind-of-STEM school could look like, we mentioned something we dubbed "The Japanese Method" of teaching math — structured group problem-solving.
Pics or it didn't happen!
That, at least, was the response of one reader. What does "structured group problem-solving" actually look like?
Today: one of the most glorious ideas alive today in math instruction. (Note: all this is stolen shamelessly from the book The Teaching Gap: Best Ideas from the World's Teachers for Improving Education in the Classroom, by James W. Stigler & James Hiebert. If you haven't a copy, buy one — it's that eye-opening!
In short: great mathematics is a culture, not just a method — but methods can help carry cultures.
The gist: before showing students how to do a type of problem, just present them the problem, and let them struggle with it.
Start by letting them struggle by themselves. Then (often, though not always) let them struggle in small groups.
As they struggle, stroll around the classroom, noting how different groups have solved the problem in different ways. Make notes of a few different methods, and invite the creators of those methods to present them on the board.
Start with confusion. Spin understanding out of chaos.
An example, you say? Let's!
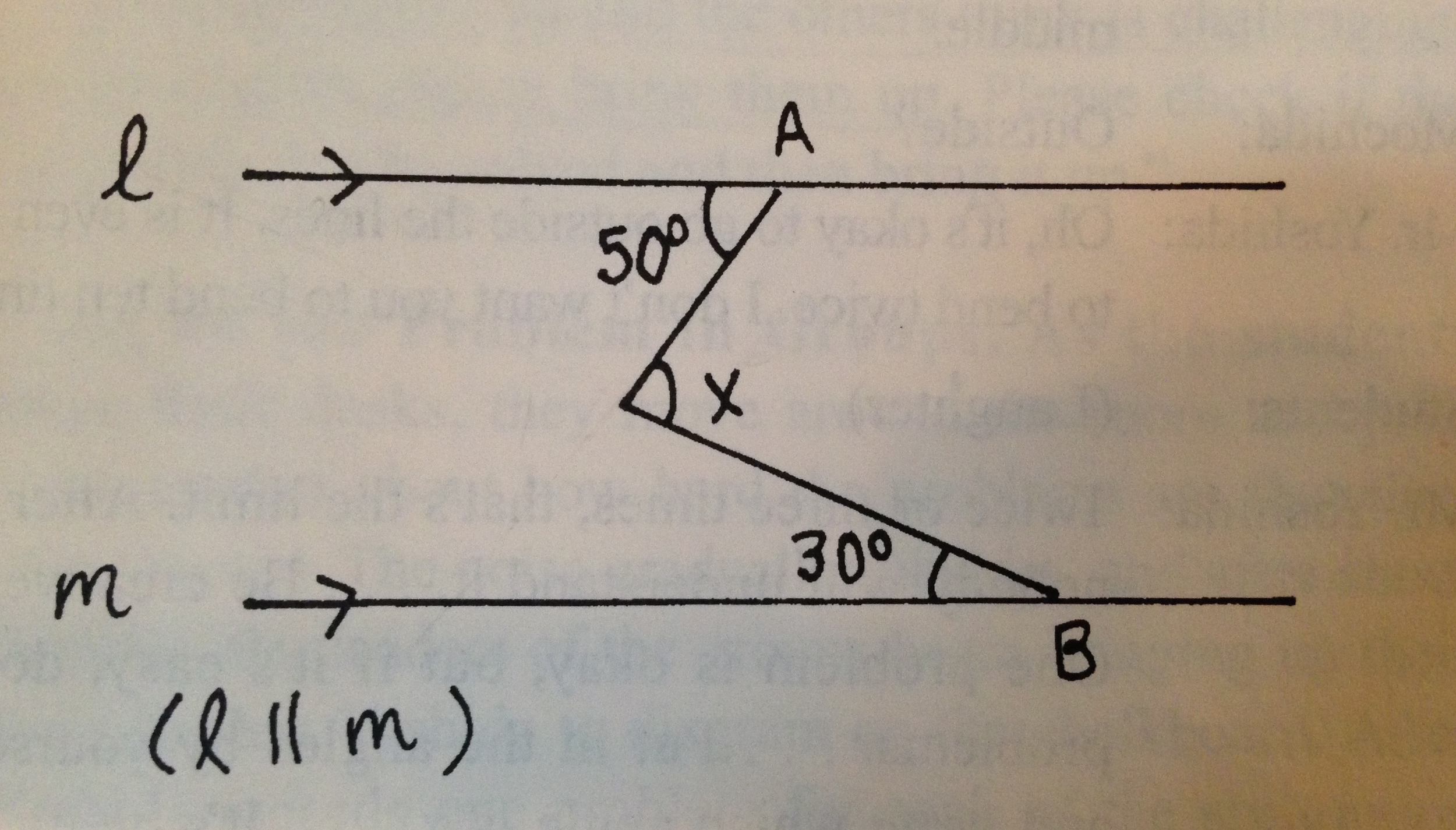
Try this problem on your own. Find x:
If you're bamboozled, good! I'm a math teacher, and I was stumped when I saw this.
If it helps, here are a few basic geometry rules the kids would be familiar with:
- There are 180º in a half turn (or "in a line") — so the fat angle above 'B' would be 150º, and the fat angle below 'A' would be 130º.
- There are also 180º in a triangle (or "three-pointed-three-liney-thing").
Let's pretend we gave this problem to a class of students.
First, we'd let them puzzle it over on their own. A minute or two might suffice.
Then, we might ask them to form small groups, and share what happened. What did they try? What did they find? What questions do they have?
As they chat, we (the teacher) would stroll about the room, noting different methods kids have come up with.
Let's assume we witness three different methods. After a few minutes, we ask a few students (let's call them Josh, Dana, and Sanket) to come to the board and share what they figured out.
Josh's Method
What did Josh do? He stretched out a line, and made a triangle — yay, triangles! Triangles are simple, and as previously mentioned, we know stuff about them — like that their inside angles add up to 180º.
Josh has labelled that top-left angle "30º", because it matches the 30º angle in the bottom right. (This is a cool previous pattern that they kids would come into this class already knowing.)
How big is that remaining angle? Well, we have the two other angles in that upper-triangle: 50º and 30º. And 50 + 30 = 80. So the remaining angle has to be 100º.
And our blessed x is smack up against that 100º angle, so it has to be 80º.
Well, done, Josh.
Now, much American math instruction would stop here: we've figured out x, after all! But is Josh's method the only way to solve the problem? Heck no!
A standard Japanese math lesson would progress to Dana's explanation.
Dana's Method
What did Dana do? She decided to drop a line straight down, and make two triangles — right triangles. If triangles are magic, then right triangles are even... magicaler?
Dana can quickly figure out the missing angles in these new triangles, because she recalls that the angles inside a triangle always add to 180º.
Using this, she finds that one angle is 40º, and the other is 60º.
Now she has a half turn (aka a "line") — 40º, xº, and 60º. Together, they have to equal 180º — so x must be 80.
Well done, Dana!
Even a quite progressive American-style math teacher might stop here. They've done their job: they've demonstrated to their students that math is creative, and that there isn't just one solution method.
Not our Japanese math teacher. Demonstrating a plurality of methods — student-originated methods — is the norm. So let's move onto Sanket.
Sanket's Method
Whoa: weird.
What's Sanket up to here? Well, like Dana, he decided to just drop a line down from the top to the bottom. But unlike Dana, he didn't make two triangles — he made one four-sided shape.
It's an interesting move. Four-sided shapes ("quadrilaterals", but aren't our lives already complicated enough?) are more complex then triangles. On the other hand, he just has one of them, rather than Dana's two triangles.
Then he gets to labeling: one angle is 130º, and another is 90º. A third angle is 60º. And the final angle is, of course, x.
Sanket recalls one thing about four-sided shapes: their angles add up to 360º. And so he adds 130 + 90 + 60 + x = 360, and finds (drumroll!) that x = 80!
Well done, Sanket!
To sum up:
This "structured group problem-solving method" starts with hard questions. (American math classes, by contrast, typically start by explaining "what to do".)
This method forces students to think for themselves, and then to think with peers. (American math classes typically start by forcing students to follow the teacher and book.)
And this method demonstrates that math is a creative, flexible pursuit — an art as well as a science. (American math classes typically demonstrate that math is about following set procedures — like filling out taxes.)
Is this method dangerous?
There is, I think, a very sensible apprehension that many of us might have to this method — that while students may learn the creative possibilities of math, they won't learn what works best.
There may be, for example, three different ways to solve the problem above, but students will benefit from learning the most efficient way.
This is an even more potent objection when we're teaching foundational processes — like adding, subtracting, multiplying, or dividing.
In our next post, I'd like to address this concern head on.